Taylor series for sine or sinus

Taylor series are great approximations of complicated functions using polynomials. This is done by replacing the actual function with polynomials that have the same derivatives as the original function. As the number of derivatives that a polynomial has in common with a specific function increases, so does the accuracy of the representation. Here I look at a very popular use of a Taylor series: the approximation of sine or sinus. All of the regular calculus functions can be approximated this way around the point x=0. For sine, we can get a fairly accurate representation of the actual function by using a polynomial at the 7th power of x for the range between -π/2 to π/2. The picture of the function covers the entire picture of sine, so by moving and/or mirroring the values by multiples of π, we can calculate sine for any value.

The Taylor series for sine looks like this: Y = X - X³/ 3! + X⁵/ 5! - ... + (-1)⁽ⁿ⁺¹⁾ * X^(2*n-1)/ (2n-1)!
Where n is any natural number. The higher you go- that more accurate the representation becomes- as we shall see in the following diagrams.

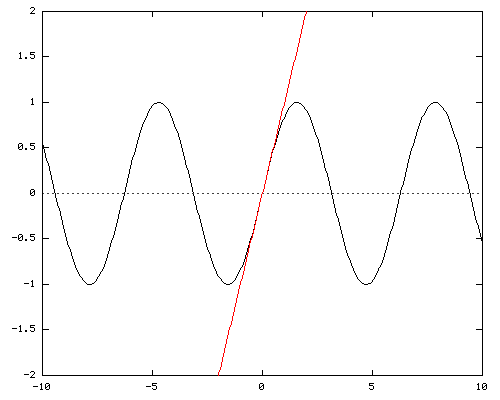
Y = X
Here we see the sine function in black, and the line Y = X in red. This line is the Taylor series for sine to a factor of 1, because the slope of sin(x) at x=0 is 1 and therefore it's derivative is also 1 at the same point. This approximation is actually not so bad for values where x is very close to 0 and accuracy is secondary to the ability to calculate quickly (think physics exams).

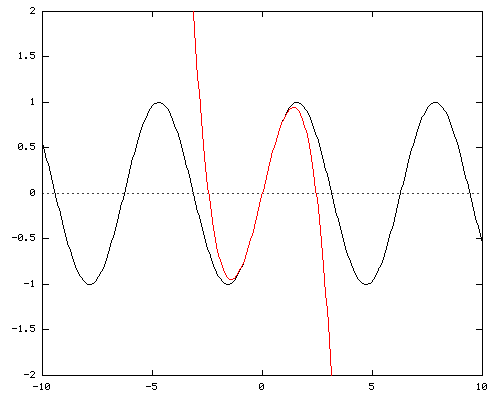
Y = X - X³/ 3!
In this image we have the Taylor series show to a power of 3. Note that there is no Taylor series powers for even numbers for sine. The graph shows that the approximation is already accurate beyond π/4.

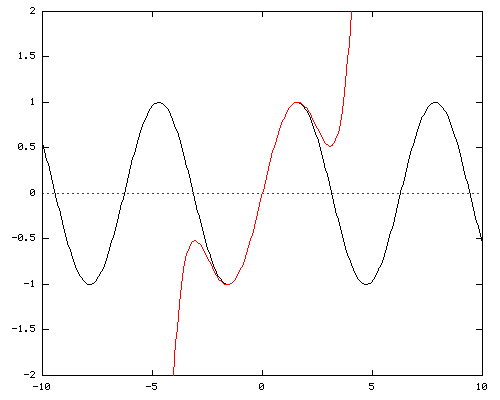
Y = X - X³/ 3! + X⁵/ 5!
At the fifth power, the Taylor series for sine is accurate up to π/2.

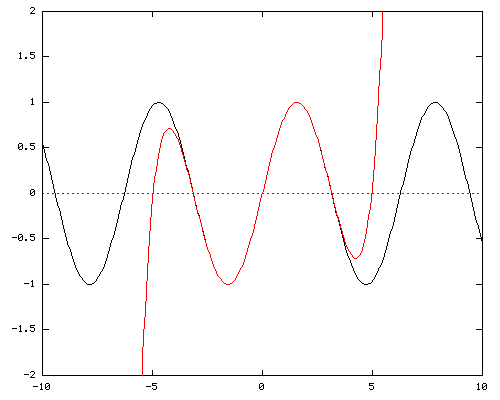
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7!
The seventh power of the Taylor series for sine is considered to be accurate enough to calculate any value of sine. The graph depicted here shows no difference between the functions for the entire range between -π/2 to π/2.

Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9!
For accurately calculating sine very close to π/2 the ninth power of the Taylor series is sometimes preferred over the seventh.

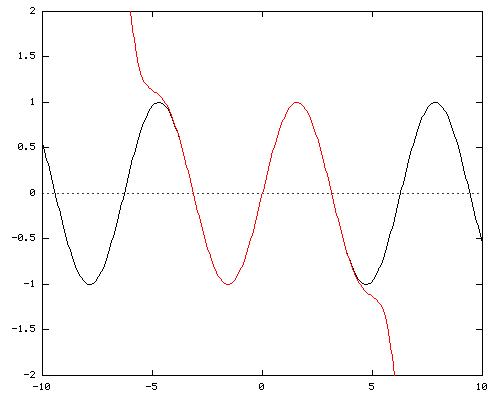
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11!
The 11^th power of the Taylor series is accurate even beyond π. This saves some work for those who prefer derivatives over mirroring functions!

Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11! + X¹³/ 13!
The 13^th power has no real advantages over the 11^th power, and has little significance.

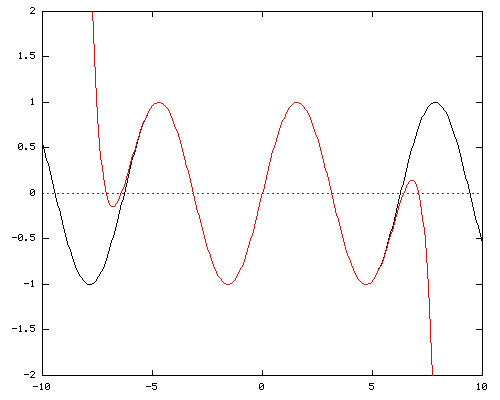
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11! + X¹³/ 13! - X¹⁵/ 15!
The 15^th power gets over the π*3/2 hump, but that doesn't really contribute anything useful.

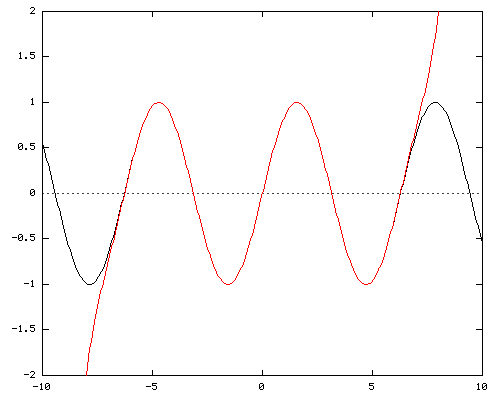
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11! + X¹³/ 13! - X¹⁵/ 15! + X¹⁷/ 17!
The 17^th power comes very close to covering sine's entire cycle of 2*π.

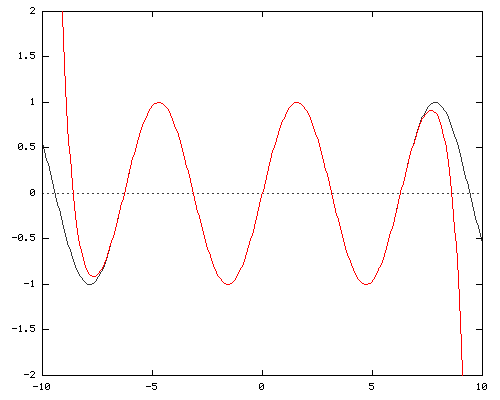
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11! + X¹³/ 13! - X¹⁵/ 15! + X¹⁷/ 17! - X¹⁹/ 19!
As does the 19^th power.

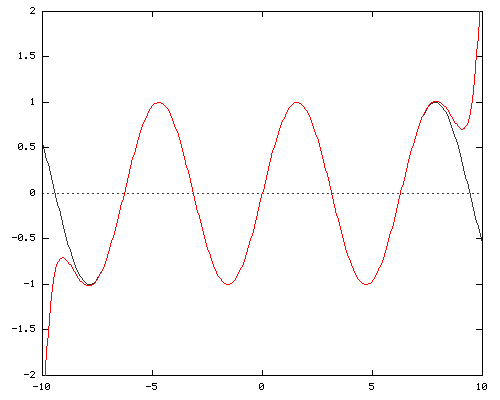
Y = X - X³/ 3! + X⁵/ 5! - X⁷/ 7! + X⁹/ 9! - X¹¹/ 11! + X¹³/ 13! - X¹⁵/ 15! + X¹⁷/ 17! - X¹⁹/ 19! + X²¹/ 21!
The 21^st power of the Taylor series for sine covers the entire cycle of 2*π. Anybody who wants to study this further, be my guest. I'm going to go break my fingers on a nice tall Pascal triangle now.

All images adapted from WIMS Function Calculator and edited using GPL-licensed tools.